Kinetic Molecular Theory
The gas laws developed by Boyle, Charles, and Gay-Lussac are based upon empirical observations and describe the behavior of a gas in macroscopic terms, that is, in terms of properties that a person can directly observe and experience. An alternative approach to understanding the behavior of a gas is to begin with the atomic theory, which states that all substances are composed of a large number of very small particles (molecules or atoms). In principle, the observable properties of gas (pressure, volume, temperature) are the consequence of the actions of the molecules making up the gas.
The Kinetic Molecular Theory of Gases begins with five postulates that describe the behavior of molecules in a gas. Some of these postulates are based upon simple, basic scientific notions, while others provide simplying assumptions. In reading a postulate, do two things. First, try to understand and appreciate the basic physical idea embodied in the postulate. This idea will ultimately be important in understanding the macroscopic properties of the gas in terms of the behavior the microscopic molecules making up the gas. Second, identify possible weakness or flaws in the postulates. Inaccurate predictions by a theory are often a consequence of flawed postulates used in the derivation of the theory.
Postulates
- A gas consists of a collection of small particles travelling in straight-line motion and obeying Newton's Laws.
- The molecules in a gas occupy no volume (that is, they are points).
- Collisions between molecules are perfectly elastic (that is, no energy is gained or lost during the collision).
- There are no attractive or repulsive forces between the molecules.
- The average kinetic energy of a molecule is 3⁄2 k T. (T is the absolute temperature and k is the Boltzmann constant.)
The Ideal Gas Law ( P V = n R T) is a consequence of these postulates. The fact that real gases do not behave ideally indicates one or more deficiencies in the above postulates.
Molecular Dynamics Simulation
Molecular Dynamics Simulations will be used to explore the behavior of molecules in a gas. In some respects, the simulations implement the postulates of the Kinetic Molecular Theory. The Molecular Dynamics Simulations treat all molecules as obeying Newton's laws of motion. The collisions are all perfectly elastic (within the numerical precision of the calculations). The simulation uses the average kinetic energy of the molecules to calculate the temperature (Postulate 5).
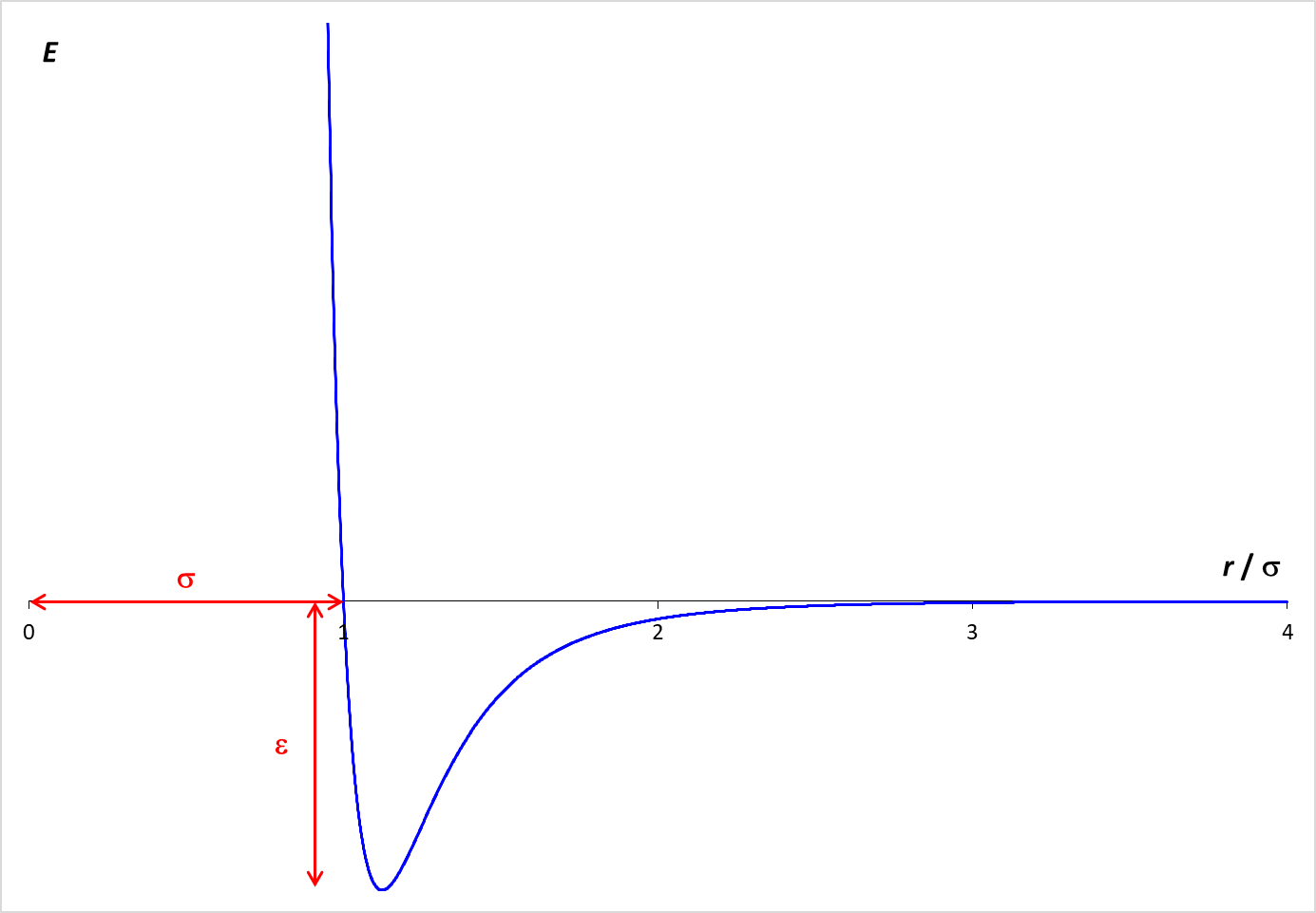
On the other hand, the simulations provide for forces between molecules. These intermolecular forces are described by the Lennard-Jones potential, which is graphed below. The graph shows how the potential energy (PE) between two molecules varies with the distance between the molecules (r). When the molecules are far apart, the PE is essentially zero. As the molecules get closer, there is an attractive force between the molecules, which lowers the PE. The particles need to be fairly close together for this attraction to be relevant. In the simulation, the molecular diameter is σ. Examination of the graph shows that the particles need to be within about two diameters (2 σ ) for a significant attractive force to exist. However, if the molecules get too close (closer than one diameter), the PE increases rapidly. This strong repulsive force drives molecules away from each other.
Behavior of a Single Molecule
To understand the behavior of molecules predicted by the Kinetic Molecular Theory, consider the box containing a single molecule, as shown below.
Start the simulation and observe the molecule, represented by the red ball, bouncing and travelling back and forth across the box. The collisions with the walls are perfectly elastic. Energy is neither gained nor lost from the collision. Because the walls do not move, the molecule's speed is unaffected by the collision. The graph plots the molecule speed as a function of time. Observe that the speed has a constant value.
Behavior of a Multiple Molecules
The next simulation involves multiple molecules. Start the simulation and observe the red molecule. The graph shows how the speed of the red molecule changes with time.
Watch the red molecule and examine the graph of its speed over time. Does the molecule follow straight-line motion? Why or why not?
What causes the speed of the red molecule to change?
Does the red molecule need to collide with another molecule for its speed to be affected by the other molecule?
Review the postulates of the Kinetic Molecular Theory. Which postulates are obeyed in the Molecular Dynamics Simulation? Which postulates are not obeyed?
Averaged over a long period of time, the average kinetic energy of a given molecule is 3⁄2 k T. Similarly, the average kinetic energy of a large number of molecules at a particular instant in time is 3⁄2 k T.
MDS-KMT.html (version 3.0)
© 2001, 2014, 2023 David N. Blauch