Chemical Equilibria
Calculation of the Equilibrium State
Consider the following reaction, which is an important atmospheric reaction.
O2 (g) + 2 SO2 (g) 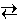 2 SO3 (g)
2 SO3 (g)
Suppose the system initially contains only oxygen and sulfur dioxide. As the reaction progresses, sulfur trioxide is formed and oxygen and sulfur dioxide are consumed. The pressure of the system is the sum of the partial pressures of the components of the gas. At equilibrium, each of these partial pressures differs from the initial values.
P = PO2 + PSO2 + PSO3
Describing the final equilibrium state requires taking the stoichiometric relations into account.
A useful concept for this purpose is the extent of reaction, which will be given the symbol x for this experiment. Each unit of x corresponds to the number of molecules of each reactant and product indicated by the respective stoichiometric coefficients. Thus when x = 1, one mole of oxygen and two moles of sulfur dioxide have been consumed and two moles of sulfur trioxide have been formed. When x = 0.1, 0.1 mole of oxygen and 0.2 mole of sulfur dioxide have been consumed and 0.2 mole of sulfur trioxide have been formed. The sense of the change can be reversed. When x = -1, one mole of oxygen and two moles of sulfur dioxide have been formed and two moles of sulfur trioxide have been consumed.
The extent of reaction allows the change in amount of one reactant or product to be related to the change in the amount of a different reactant or product. One way to illustrate this relationship is through the use of a table such as that shown below.
| Calculation Step | O2 | SO2 | SO3 |
|---|---|---|---|
| Initial | P1 | P2 | P3 |
| Change | - x | - 2 x | + 2 x |
| Equilibrium | P1 - x | P2 - 2 x | P3 + 2 x |
Strictly speaking, the table should be constructed in terms of moles of each species. The equilibrium expression, however, requires partial pressures or molar concentrations. So long as each species exists in the same phase (and thus the volume is the same for each species), the moles can be replaces by partial pressure or molar concentration. In this example the extent of reaction is expressed in terms of partial pressure.
There is a column for each reactant or product in the chemical reaction that appears in the equilibrium expression. The entries under a chemical species apply to that specific species.
The first row of the table contains the initial partial pressures of each species. These values are called "analytical partial pressures" and are the partial pressures of each species based upon what the experimenter put in the system.
The second row expresses the stoichiometry of the reaction and employs the extent of reaction to show how the change in amount of one reactant or product is linked to the changes in the amounts of the other reactants and products. Each entry in this row consists of the extent of reaction multiplied by the stoichiometric coefficient for the species at the top of the column. The expression is positive for products and negative for reactants.
The bottom row is simply the sum of the first two rows and contains the actual equilibrium partial pressures of each species. In this context, the extent of reaction, x, is the value necessary to reach equilibrium. At equilibrium, the values in the bottom row of the table may be substituted into the equilibrium expression to evaluate KP. Or, if KP is known, the equilibrium expression can be used to determine the value of x.
- Can you calculate the value of x if you are given the pressure P and the three initial partial pressures P1, P2, and P3?
- Can you calculate the individual partial pressures and the equilibrium constant, if you are given x and the three initial partial pressures P1, P2, and P3?
- Will this strategy for determining KP from P work for the reaction shown below? Explain.
CO (g) + H2O (g) 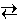 CO2 (g) + H2 (g)
CO2 (g) + H2 (g)
Experiment: Part 1
In this part of the experiment, you will determine the equilibrium constant for the following chemical reaction:
O2 (g) + 2 SO2 (g) 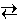 2 SO3 (g)
2 SO3 (g)
The experimental apparatus consists of a pair of glass bulbs. The bulb on the left is first evacuated and then filled with a certain amount of oxygen. The pressure of the oxygen is measured with the manometer on the left. Similarly the bulb on the right is evacuated and then filled with a certain amount of sulfur dioxide, the pressure of which is measured with the manometer on the right.
The reaction occurs when the stopcock between the two bulbs is opened, allowing the gases to mix. At this stage, either manometer may be used to measure the equilibrium pressure of the system.
Perform this experiment several times using various initial pressures of oxygen and sulfur dioxide gas. You should obtain the same value for KP each time ... within experimental error(!)
Each bulb has a volume of 1.000 liter. (Note that this reaction is performed at a high temperature.)
Note: The pressures you measure for oxygen and sulfur dioxide while the stopcock between the bulbs is closed are NOT the quantities P1 and P2 in the table shown above. Why is this the case? How can you calculate P1 and P2?
Small errors in measuring the equilibrium pressure produce large errors in the value for KP. At best, the manometers can only be read to about 1%, but this error can produce much larger errors in KP. This effect of small errors in one quantity producing errors in a computed quantity is called propagation of error. For this reason, the manometer pressure is shown to higher accuracy and precision below each manometer. This allows much more accurate determination of the equilibrum constant.
After performing the experiment a few times, you may check your answer to see if your calculations are correct.
Oxygen
Sulfur Dioxide
Experiment: Part 2
In this part of the experiment, you will determine the equilibrium constant for the reaction used by industry to synthesize ammonia (the Haber process).
3 H2 (g) + N2 (g) 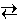 2 NH3 (g)
2 NH3 (g)
The experimental apparatus and the procedure are the same as those in Part 1. As before, each bulb has a volume of 1.000 liter. You goal is to determine the equilibrium constant ( KP ) for this reaction at 400 K.
As before, repeat the experiment several times to determine the reproducibility of your value for the equilibrium constant. In this part of the experiment, the value of KP is not provided.
Hydrogen
Nitrogen
ReactionTable.html version 3.0
© 2001, 2014, 2023 David N. Blauch